去年一直都没有写过一篇赛后的题解啊什么的,今年就当复习好了。
NOIP 2016
因为2016之前做过NOIP 2015,产生了一种NOIP很简单的错觉…
这是NOIP 2015

这是NOIP 2016

这个D1T2不知道刷掉了多少顺着做题,每题死磕的人。话说为什么天天爱跑步还不加入大牛分区…
1.1 玩具谜题
模拟题就不用多说了吧?别写错就行了。
代码:
#include <bits/stdc++.h>
using namespace std;
int n, m, cur, face[MAXN];
char name[MAXN][100];
int main() {
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i++) {
scanf("%d%s", &face[i], &name[i]);
}
for (int i = 0; i < m; i++) {
int dirc, dis;
scanf("%d%d", &dirc, &dis);
if((face[cur] == 0 && dirc == 0) || (face[cur] == 1 && dirc == 1)) {
cur -= dis;
}
else if((face[cur] == 0 && dirc == 1) || (face[cur] == 1 && dirc == 0)) {
cur += dis;
}
if(cur < 0) cur += n;
if(cur >= n) cur -= n;
}
printf("%s\n", name[cur]);
return 0;
}
1.2 天天爱跑步
说它是NOIP 2016最难的一题没意见吧,很多人都以为NOIP的难度是顺着来的,事实上很多大佬和集训机构也说“NOIP一天三道题难度坡度区别明显”,这次也很明显,但不是直角梯形的坡度,是三角形的坡度。
题目大意:在一张N个节点的树上有M个人,每个人有自己的终点。他会选择最短的路跑到自己的终点。这棵树上每个点都有一个检测装置,检测装置只会在特定的时间开启一次,记录下来刚好经过的人。每个人第0秒都在自己的起点上,从一个点跑到相连接的另一个点耗时1s,请问每个检测点记录的人数。
乍一看,路径还原随便搞搞,但是看到了数据范围如此之惊人,发现并没有那么简单。
先做一点铺设:我们如何快速地给一整条链添加信息?需要从链头遍历到链尾吗?时间复杂度肯定是接受不了的。所以有一种操作被引入了,我们可以仿照数组的后缀和的思想来处理这个问题。例如,如果我想在 \([l, r]\) 这个区间给每个点添加一个信息v,那么就可以给\(l - 1\)打上一个减标记,\(r\) 打上一个加标记,这样的话对于每个点求它的后缀和就是点上所有的信息了。
举一个树上的例子: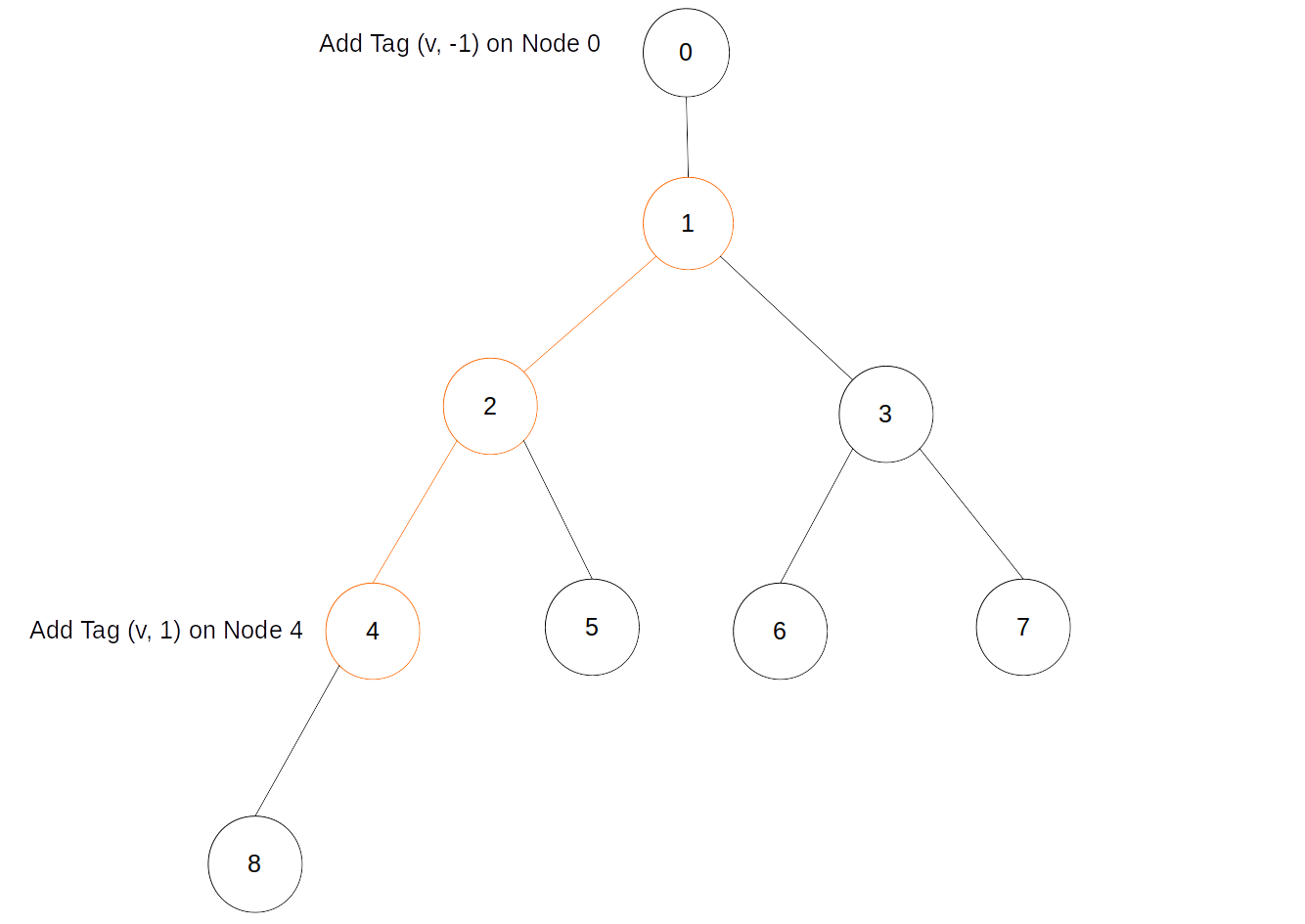
如图,我们要给1-2-4这条链整链加上一个信息,那么我们就只用在1的父亲、4这两个节点分别打上相应的标记就可。当统计信息时,假如统计2的信息,那么只用求它的(包括当前节点的)子树和就可以了。对于不属于这条链上的任意一个点,所求得之结果均为Nothing。
如果链有重叠呢?是一样的,比如:

这次我们想给2-4-8这条链赋予信息,仿照刚才的做法,我们在1和8两个节点打上减标记和加标记。这时候,2这个节点应该既有第一条链的信息也有第二条链的信息吧。事实求得子树和也如此,是很显然的。而对于1来说,它只有第一条链的信息,没有第二条链的信息,我们来看一下它的(包括当前节点的)子树和:一个第一条链的加标记,一个第二条链的加标记,一个第二条链的减标记。所以综上,结果依然正确。
对这道题有什么帮助呢?有的,就看理解不理解的了了,反正我当初看大佬们写的博客的时候还是很懵的。
先考虑起点到终点是一条链的情况,抛砖引玉一下:
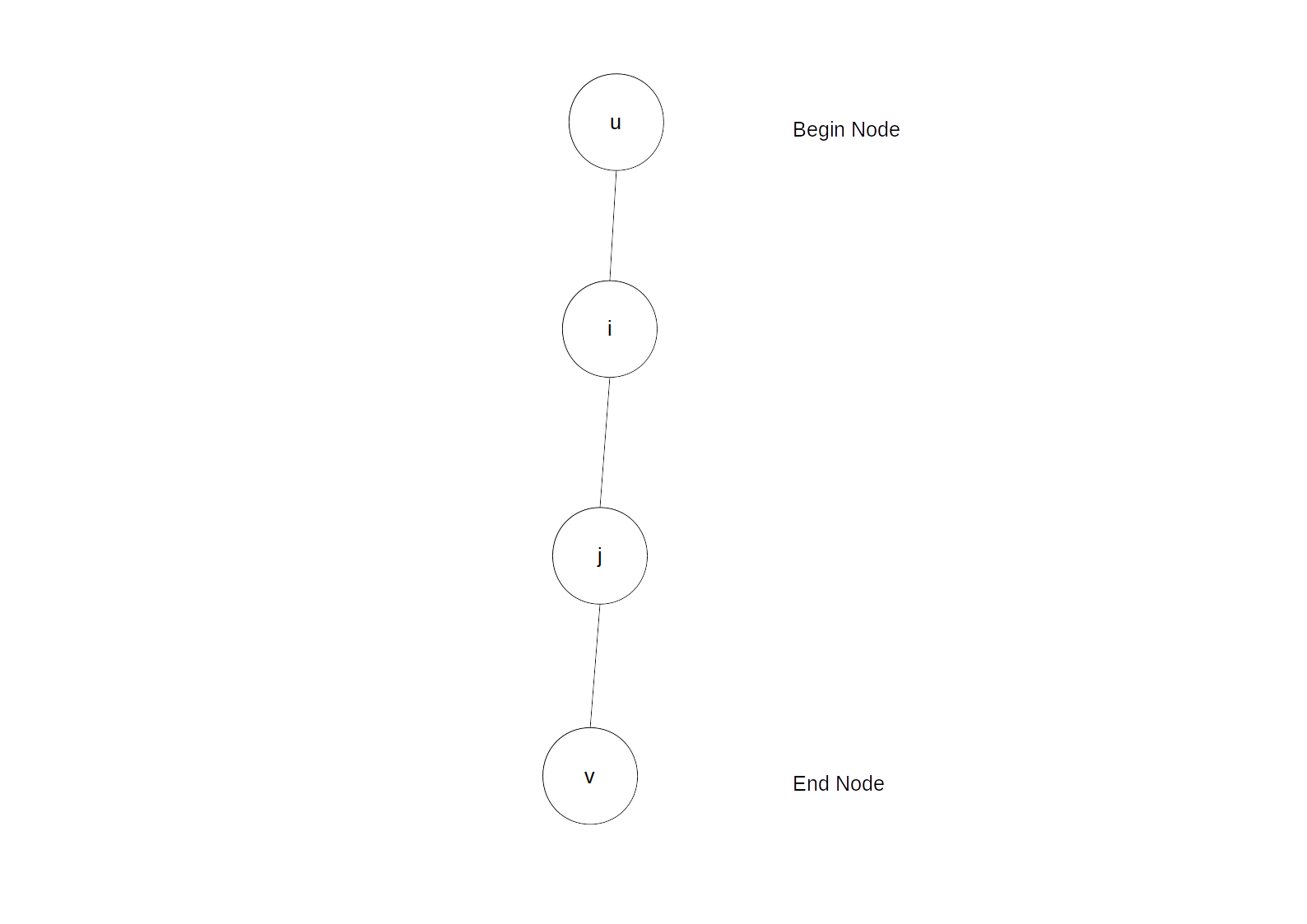
\(u\)是起点,\(v\)是终点。\(i,j\)是中间点。题目中说每个点都有一个检测机制,它们的检测时间用一个数组\(w[]\)存下来。现在我们假定这个人从\(u\)出发向下爬。那么对于链上的每个点,能否检测到人的条件就是\(depth[k] - depth[u] == w[k]\) (k为当前点)。然后你会发现\(depth[k] - w[k]\) 是每个点的一个特征值,是确定的。换句话说,对于每个监测点,也就是每个点,我们检查一下有没有\(depth[u]\)等于这个值,再看一下\(u\)这个点出发的人(如果存在)经不经过这个\(k\)点?
这时候结合刚才的标记方法,我们有个思路:给\(u\rightarrow v\)这条链打上一个标记,标记的值为$depth[u]$,然后,对比每个点自己的一个特征值,如果两者相等,即为满足前文所提到的条件,那么就当前点的值+1。
这是“向下走”的链的做法,向上走的其实也差不多,只是移项的时候符号不同而已。所以每次要保存两个值记录向上走偶遇或者向下走偶遇的情况。只用多出来一个数组就OK。
既然链的方法可以这样做(本题已经可以拿到40分了),那么对于一般性的带弯折的一条路径怎么办呢?可以求出起点与终点的LCA,然后再将其路径从LCA处拆成两端,仿照上文所提的方法进行统计。对于本题,我们不需要求出任意两点之间的LCA,对于给定一张图多次询问两点之间的LCA的问题用Tarjan算法就可以在\(O(N+Q)\)的时间内解决。
综上所述,这就是完整思路。具体代码的话…其实我的代码也是看各位大佬的博客拼凑起来的,如果仍然下不了键盘可以去看一下题解…然后顺着想一下大佬们是怎么考虑问题的。这道luogu的各位给出省选/NOI-的题肯定还是有一定难度的。去年我就是只拿了个暴力25分遁走的人
1.3 换教室
一道比第二题简单的第三题,最近几年很少见…
首先要了解期望的可加性,因为和的期望等于期望之和,所以可以感觉到每一步选择换或者不换是由上一步的期望和加上某个值而来的。这样的话就只用考虑当前的选择和上一步的选择就可以了。注意到数据范围很小,\(v \le 300\),所以我们可以用Floyd算法求出任意两点之间的最短路。注意Floyd的时候三个循环上界都是\(v\)不是\(n\)也不是\(2n\),教室是可以反复利用的…这里卡了好久。
因为刚刚所说的每一步的取值都之与最后两步相关,所以我们很容易得出来一个换教室和不换教室的dp。
对于dp数组\(f[i][j][k]\),表示当前考虑到第\(i\)个点,前\(i-1\)个点中已经选了\(j\)个,且当前点是否选择换教室,0不换,1换。那么对于当前不换教室,可以得出:
\[f[i][j][0] = min\begin{cases} f[i-1][j][0] + d[a[i - 1]][a[i]]\\ f[i-1][j][1] + p[i - 1]\cdotp d[b[i - 1]][a[i]] + (1 - p[i - 1])\cdotp d[a[i - 1]][a[i]] \end{cases}\]如果要换的话可能就要麻烦点:
\[f[i][j][1] = min \begin{cases} f[i - 1][j - 1][0] + p[i]\cdotp d[a[i - 1]][b[i]] + (1 - p[i])\cdotp d[a[i - 1]][a[i]] \\ f[i - 1][j - 1][1] + p[i - 1]\cdotp p[i] \cdotp d[b[i - 1]][b[i]] + (1 - p[i - 1]) \cdotp p[i] \cdotp d[a[i - 1]][b[i]] + p[i - 1] \cdotp (1 - p[i]) \cdotp d[b[i - 1]][a[i]] + (1 - p[i - 1]) \cdotp (1 - p[i]) \cdotp (d[b[i - 1]][b[i]]) \end{cases}\]这一串写的真的头皮发麻…但是还是很好理解的,无非是概率的乘法法则和期望的可加性。
注意一下,别的平台不知道,luogu的数据里有自环和重边。
代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 2010, V = 310;
int a[N], b[N];
double d[V][V];
double c[N];
double f[N][N][2];
int cnt = 0;
int n, m, v, e;
void init() {
for (int i = 0; i < V; i++)
for (int j = 0; j < V; j++)
if (i == j) d[i][j] = 0;
else d[i][j] = 1e9;
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
f[i][j][0] = f[i][j][1] = 1e9;
f[1][0][0] = 0; f[1][1][1] = 0;
}
void floyd() {
for (int k = 1; k< = v; k++)
for (int i = 1; i< = v; i++)
for (int j = 1; j< = v; j++)
if (d[i][k] + d[k][j] < d[i][j])
d[i][j] = d[i][k] + d[k][j];
}
int main()
{
scanf("%d%d%d%d", &n, &m, &v, &e);
for (int i = 1; i< = n; i++) scanf("%d", &a[i]);
for (int i = 1; i< = n; i++) scanf("%d", &b[i]);
for (int i = 1; i< = n; i++) scanf("%lf", &c[i]);
init();
for (int i = 1; i< = e; i++) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
if (x == y) continue;
if (z < d[x][y]) d[x][y] = d[y][x] = z;
}
floyd();
for (int i = 2; i< = n; i++) {
f[i][0][0] = f[i - 1][0][0] + d[a[i - 1]][a[i]];
for (int j = 1; j <= min(m, i); j++) {
f[i][j][0] = min(f[i - 1][j][0] + d[a[i - 1]][a[i]], f[i - 1][j][1] + d[a[i - 1]][a[i]] * (1.0 - c[i - 1]) + d[b[i - 1]][a[i]] * c[i - 1]);
f[i][j][1] = f[i - 1][j - 1][0] + d[a[i - 1]][a[i]] * (1.0 - c[i]) + d[a[i - 1]][b[i]] * c[i];
double t = f[i - 1][j - 1][1] + d[a[i - 1]][a[i]] * (1.0 - c[i - 1]) * (1.0 - c[i]);
t += d[b[i - 1]][a[i]] * c[i - 1] * (1.0 - c[i]);
t += d[a[i - 1]][b[i]] * (1.0 - c[i - 1]) * c[i];
t += d[b[i - 1]][b[i]] * c[i - 1] * c[i];
f[i][j][1] = min(f[i][j][1], t);
}
}
double ans = f[n][0][0];
for (int i = 1; i <= m; i++) {
ans = min(ans, min(f[n][i][0], f[n][i][1]));
}
printf("%.2lf", ans);
return 0;
}
2.1 组合数问题
算是比较正常的一题了。
题目大意:给定\(n, m, k\)三个数,要求计算出:\(\sum_{i=0}^n\sum_{j=0}^{min(i,m)}\big[ k \mid C_i^j\big]\) .
首先用DP算出组合数(杨辉三角),然后再用前缀和或容斥的思想计算出每一个具体的 \(i,j\) ,即可复杂度\(n^2\) ,\(n^3\)暴力有70分。
状态转移方程:
\[C[i][j] = C[i][j - 1] + C[i - 1][j - 1]\] \[S[i][j] = \big[ j \le i \ \ \&\ \ C[i][j] == 0 \big] + sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1]\]对于每个\(n,m\)询问,答案就是\(sum[n][m]\)。
代码:
#include <bits/stdc++.h>
using namespace std;
const int MAX_N = 2000 + 5, MAX_M = 2000 + 5;
int K, c[MAX_N + 3][MAX_N + 3], s[MAX_N + 3][MAX_N + 3];
void process() {
memset(c, 0, sizeof c);
memset(s, 0, sizeof s);
c[0][0] = 1;
for (int i = 1; i < MAX_N; ++i) {
c[i][0] = c[i][i] = 1;
for (int j = 1; j < i; ++j)
c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % K;
}
for (int i = 1; i <= MAX_N - 1; ++i)
for (int j = 1; j <= MAX_M - 1; ++j)
s[i][j] = (j <= i && c[i][j] == 0) + s[i][j - 1] + s[i - 1][j] - s[i - 1][j - 1];
}
int main() {
int caseNum;
scanf("%d%d", &caseNum, &K);
process();
while (caseNum--) {
int n, m;
scanf("%d%d", &n, &m);
printf("%d\n", s[n][m]);
}
return 0;
}
2.2 蚯蚓
看到题目描述就知道是一道非常UOJ的题…
题面很长很吓人,再加上昨天鬼畜般的题目难度顺序安排,不禁心里一抖,但再一仔细看,莫非是道模拟题?
题意大致如下:有\(n\)个数,每个数每过1s增长\(q\),而每秒钟会选出最大的一个数(如果有多个就任选一个),把它按比例向下取整分成两部分(比♂例是个常♂数)加入原数列。然后询问每过\(t\)秒选出来的数被分之前是多少,以及操作完后将所有的数按大小排序输出。
第一反应就是优先队列,可是问题是这道题的数据范围也很感人。并且luogu上好像没开O2…很多人STL被卡掉了。
换个思维。每次除了被拎出来的那个数,有很多数被加了\(q\)对不对?为什么要重复很多次加常数的操作呢?我们可以用标记的思想来考虑一下,加的数我们暂时不加,而是把被砍的那个数砍完以后减去\(q\)。这样并不会改变相对的大小顺序。最后在输出的时候,把每个数加上相应的该加的数就可以了。
代码:
//Created by uneducable
#include <bits/stdc++.h>
#define MAXN 100000 + 10
#define MAXM 7000000 + 10
using namespace std;
typedef long long ll;
inline int read() {
int w = 0, f = 1; char ch = getchar();
while ((ch > '9' || ch < '0') && ch != '-') ch = getchar();
if (ch == '-') f = -1, ch = getchar();
while (ch >= '0' && ch <= '9') w = w * 10 + ch - '0',ch = getchar();
return w * f;
}
int n, m, q, u, v, t, a[MAXN];
int s[3][MAXM], l[3], r[3];
const int inf = 0x3f3f3f3f;
inline int getMax() {
static int temp, id;
temp = INT_MIN, id = 0;
for (int i = 0; i < 3; i++) {
if (r[i] - l[i] >= 1 && s[i][l[i]] > temp) {
temp = s[id = i][l[i]];
}
}
return id;
}
void solve() {
sort(a, a + n), reverse(a, a + n);
memcpy(s[0], a, sizeof a);
memset(l, 0, sizeof l);
memset(r, 0, sizeof r);
r[0] = n;
bool pace = false;
for (int ti = 0, cur, id, lt, rt, tmp; ti < m; ti++) {
id = getMax(), cur = s[id][l[id]++];
tmp = ti * q;
if ((ti + 1) % t == 0) {
if (pace) printf(" ");
else pace = true;
printf("%d", cur + tmp);
}
lt = (ll)(cur + tmp) * u / v, rt = (cur + tmp) - lt;
lt -= tmp, rt -= tmp;
s[1][r[1]++] = lt - q; s[2][r[2]++] = rt - q;
}
printf("\n");
pace = false;
int sum = m * q;
for (int i = 0, id, cur; i < n + m; i++) {
id = getMax(), cur = s[id][l[id]++];
if ((i + 1) % t == 0) {
if (pace) printf(" ");
else pace = true;
printf("%d", cur + sum);
}
}
printf("\n");
}
int main() {
n = read(), m = read(), q = read(), u = read(), v = read(), t = read();
for (int i = 0; i < n; i++) a[i] = read();
solve();
return 0;
}
2.3 愤怒的小鸟
题意:对于一个平面直角坐标系的第一象限,有 \(n\) 个不同的点,请问你最多用多少条抛物线可以完全覆盖这 \(n\) 个点?
对,你没看错,\(m\)(在正解中)卵用没有。
首先看到 \(n \le 18\) 可能就会有状压DP的第一反应。奈何我去年这个时候没有学状压DP 23333。
预处理出 \(f[i][j]\) ,表示第 \(i\) 只猪和第 \(j\) 只猪被同时打掉的情况下还能打掉哪些猪。这里算是用了三点确定一条抛物线的性质。 \(f[i][j]\) 是个二进制表示的集合,0表示打不到,1表示可以打到。这个集合里 \(i,j\) 是肯定为1的。
然后枚举出(最多18只猪)每一种可能的状态,对于每一种可能,先固定第一只没有被打掉的猪(肯定要被打掉),然后枚举包含它的抛物线(仅包含它的和包含它和另一头猪的),来向后更新,一头猪更新后面两个状态。
代码:
#include <bits/stdc++.h>
#define MAXN 18 + 3
using namespace std;
const double eps = 1e-10;
int T, n, m;
double x[MAXN], y[MAXN];
int f[MAXN][MAXN], dp[1 << 19];
inline void work() { //这里写错卡了我一个上午
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j <= n; j++) {
double x1 = x[i], y1 = y[i], x2 = x[j], y2 = y[j];
double a = (x1 * y2 - x2 * y1) / (x1 * x2 * (x2 - x1));
double b = (x1 * x1 * y2 - x2 * x2 * y1) / (x1 * x2 * (x1 - x2));
if (a >= 0) continue;
for (int k = 1; k <= n; k++) {
double t = a * x[k] * x[k] + b * x[k];
if (y[k] - eps <= t && t <= y[k] + eps)
f[i][j] |= (1 << (k - 1));
}
}
}
}
inline int solve() {
dp[0] = 0;
for (int i = 0; i <= (1 << n) - 2; i++) {
int k = 0;
while ((1 << k) & i) k++; k++;
dp[i | (1 << (k - 1))] = min(dp[i | (1 << (k - 1))], dp[i] + 1);
for (int j = k + 1; j <= n; j++)
dp[i | f[k][j]] = min(dp[i | f[k][j]], dp[i] + 1);
}
return dp[(1 << n) - 1];
}
int main() {
scanf("%d", &T);
while (T--) {
memset(f, 0, sizeof f);
memset(dp, 0x3f, sizeof dp);
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) scanf("%lf%lf", &x[i], &y[i]);
work();
printf("%d\n", solve());
}
return 0;
}
End of All
NOIP 2016 要说难其实也不难,毕竟两天的第三题都还好,但是涉及的知识点如果没有提前学就GG,数学期望和状压DP恰好我之前都没有接触过……
总之,NOIP 2017 加油吧。
xD.