Treap是一种排序二叉树(BST),同时也满足堆的性质。Treap的由来即为Tree + Heap。
鉴于手写写不来红黑树,再加上Treap能实现一些STL的set和map实现不了的操作,因此Treap还是很有学习一个的必要的。
本文介绍的是旋转式Treap,另一种Treap请参考:非旋转式Treap
思想
如果给定一串数列,按照普通的BST建树思想,建出来的树不一定唯一。而如果给每一个数增加一个优先级呢?如果按照优先级,规定优先级小/大的节点深度也应该小/大(小根堆/大根堆),那么这棵树是唯一确定的。
现在就要考虑如何实现在BST上对节点基于优先级的重排:不能单纯的让节点“向上爬”或者交换父子节点,因为这样做会破坏BST的性质。所以就引入了一种新的操作:旋转(Rotate)。

旋转分两种操作,左旋和右旋。分别把右儿子和左儿子旋转到根的位置。并且旋转的过程中并没有破坏BST的性质:上图中,\(a<y<b \& y < x\) ,如果单纯地交换x与y,那么x与y以及x与b的位置关系明显是存在问题的。旋转的目的就是将左/右儿子作为根的同时保证它的父节点、儿子节点在正确的位置。
实现
旋转
void rotate(Node* &o, int d) {
Node *k = o->ch[d^1]; o->ch[d^1] = k->ch[d]; k->ch[d] = o; o = k;
}有时还会在旋转节点时对节点保存的信息进行更新维护:
void rotate(Node* &o, int d) {
Node *k = o->ch[d^1]; o->ch[d^1] = k->ch[d]; k->ch[d] = o;
o->maintain(); k->maintain(); o = k;
}插入
void insert(Node* &o, int x) {
if(o == NULL) {
o = new Node();
o->ch[0] = o->ch[1] = NULL; o->v = x; o->r = rand();
} else {
int d = o->cmp(x);
insert(o->ch[d], x);
if (o->ch[d]-r > o->r) rotate(o, d^1);
}
}和rotate一样,要维护信息时需要在调用递归后加一句o->maintain();
删除
插入和删除可视为逆操作。删除是要视情况而删除(如下图),若待删除节点只有一个儿子,那么直接让它的儿子取代待删除节点的“地位”即可,并且保证了Treap的性质。但如果有两个儿子,那就要选出优先级大的一个儿子,通过旋转成为“根”,然后在另一个儿子中递归被旋转下去的要删除的节点,待其满足只有一个儿子时删除之。
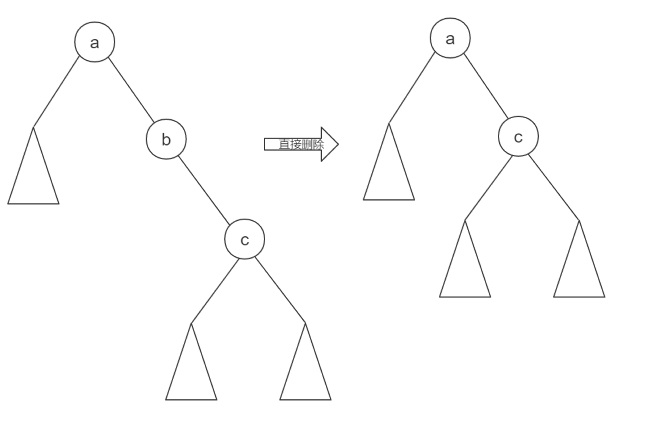
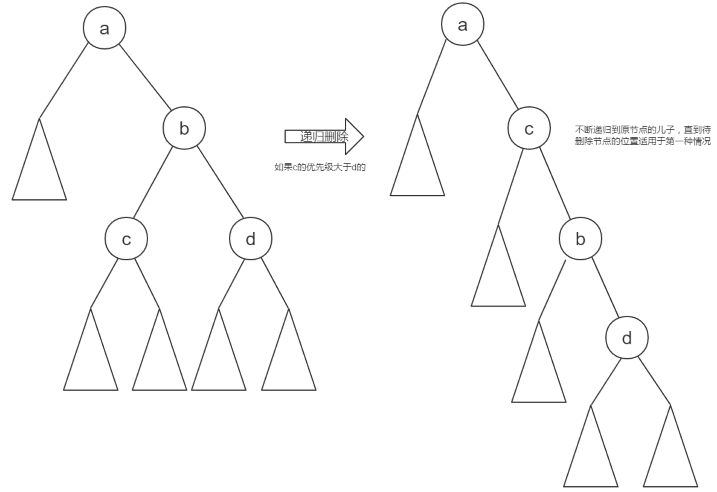
void remove(Node* &o, int x) {
int d = o->cmp(x);
if (d == -1) {
if (o->ch[0] == NULL) o = o->ch[1];
else if (o->ch[1] == NULL) o = o->ch[0];
else {
int d2 = (o->ch[0]->r > o->ch[1]->r ? 1 : 0);
rotate(o, d2); remove(o->ch[d2], x);
}
} else {
remove(o->ch[d], x);
}
}查找
int find(Node* o, int x) {
while (o != NULL) {
int d = o->cmp(x);
if (d == -1) return 1;
else o = o->ch[d];
}
return 0;
}应用
如果只是重复造一个set轮子,那么完全没有学Treap的必要。
Treap的一大作用就是,在节点添加相应信息,每次插入、删除、旋转的时候进行一下维护,那么Treap就可以实现名次树等。
方法很简单,增加一个函数maintain,和一个内部变量s。o->s = o->ch[0]->s+o->ch[1]->s
完整的结构体代码如下:
struct Node {
Node *ch[2];
int s, v, r;
int cmp(int x) {
if(x == v) return -1;
else return x < v ? 0 : 1;
}
void maintain() {
s = ch[0]->s + ch[1]->s + 1;
}
};何时维护取决于题目的具体问题,但是insert和rotate必须要插入维护语句以保证s的正确性。
完整代码
把上面每段粘起来就是完整代码。
其他
1.我上述模板采用的差不多都是汝佳的写法。但是有几点需要注意,lrj在描述旋转时,待旋转点是处于儿子地位的,但是旋转函数的操作对象是其父亲。这个在后面一节讲Splay的三种旋转时绕了我好久。
2.当维护函数maintain进行到叶子节点时,如果直接加可能会出现一定问题(NULL),解决方案是Node *null = new Node(); 手动创造一个NULL(节点),以后的函数如果可能涉及到NULL即可以用null代替。
3.旋转式的Treap和非旋转式的Treap各有好坏。前者阅读起来直观,写起来好写,理解上也不存在什么困难,但因为有了旋转操作,不是可持久化数据结构;后者虽然理解起来没有那么直观,但是码量少(主要函数20+行解决),支持持久化。
4.这篇备忘本定于9.5号写完,拖到现在是因为…算了不说。
xD.