声明:该文章仅仅为KMP算法的简单总结。如果想要更详尽的分析和过程,请参考文中的参考链接。
KMP算法简单总结
KMP是一种高效处理字符串匹配的算法,它可以在\(O(n + m)\)的时间复杂度内检测模板字符串是否被代匹配字符串所包含,并且远远优于复杂度近似为\(O(n^2)\)的朴素做法
参考
(这篇文章很水,因为我根本就不会作图…没有图学习KMP是非常痛苦的。我推荐大家参考一下Sengxian大佬以及July老师的博客。他们的博客不但有图演示了朴素算法以及KMP的匹配过程,也有非常详细的分析和代码支持。)
在这里,引用KMP的主要思想
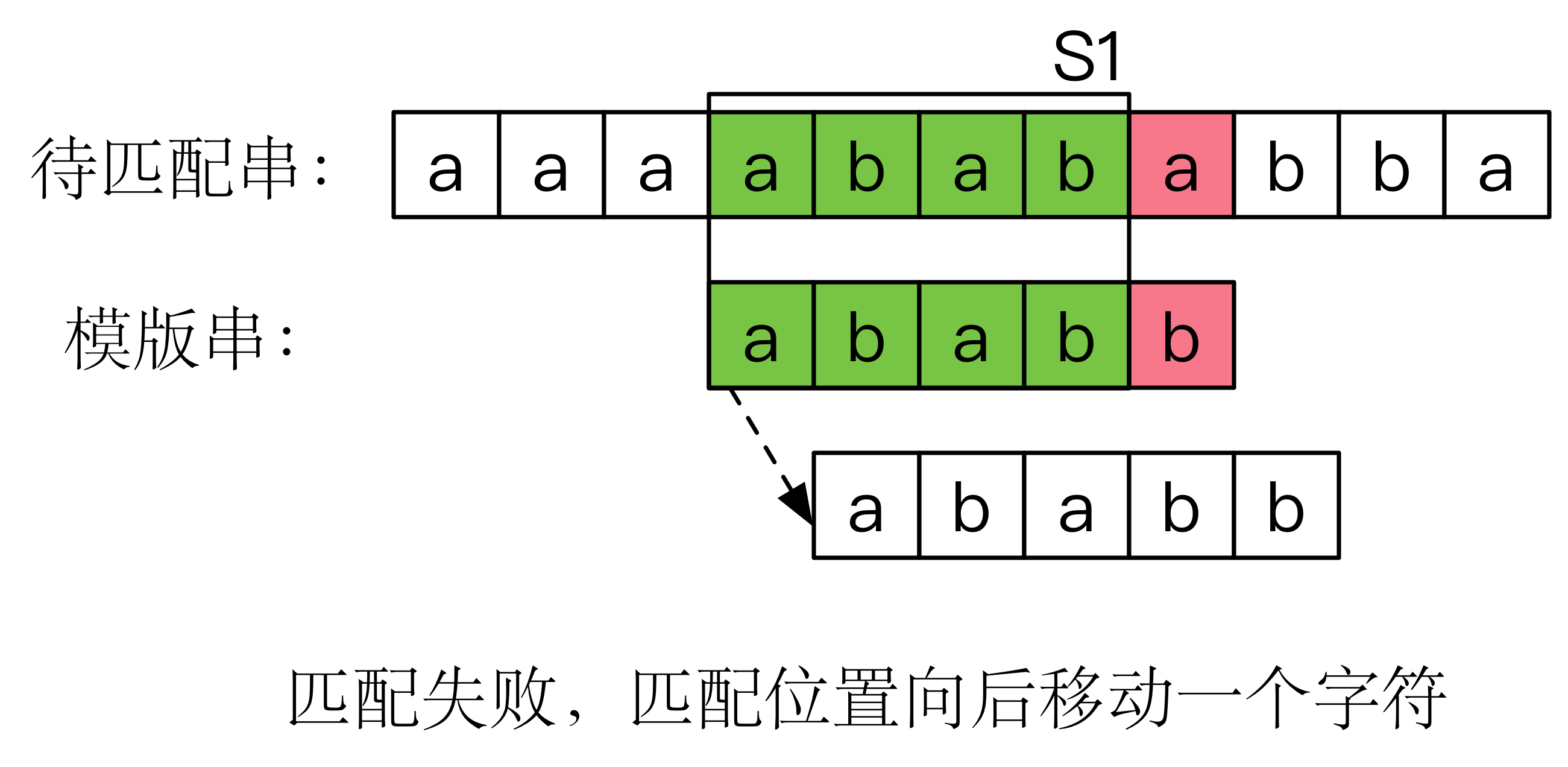
“假如在匹配的过程中发现正在比较的两个字符不同(称之为失配),那么朴素的算法会将模版串右移一位,重新比较。”
“而KMP算法认为,既然失配部分前面的字符(区域S1)已经比较过了,那么就不应该再比较一次。我们已经知道S1部分就是
abab,如果后移动一个字符,a与b肯定不能匹配。 后移2位是可以的,因为模版串的前两个字符ab正好对齐S1的后两个字符ab,我们可以发现,这样的移动跟待匹配串是没有任何关系的,只要模版串中的失配点确定,那么对应后移的位数也随之确定。”…………
其实KMP最重要的部分还是next数组的计算,这里的next数组计算用到了递推的思想,即:
- 问题是:已知next [0, …, j],如何求出next [j + 1]呢?
对于P的前j+1个序列字符:
- 若p[k] == p[j],则next[j + 1 ] = next [j] + 1 = k + 1;
- 若p[k] != p[j],如果此时p[ next[k] ] == p[j ],则next[ j + 1 ] = next[k] + 1,否则继续递归前缀索引k = next[k],而后重复此过程。 相当于在字符p[j+1]之前不存在长度为k+1的前缀”\(p_0\), \(p_1\), …, \(p_{k-1}\),\(p_k\)“跟后缀“\(p_{j-k}\), \(p_{j-k+1}\), …, \(p_{j-1}\), \(p_j\)“相等,那么是否可能存在另一个值t+1 < k+1,使得长度更小的前缀 “\(p_0\), \(p_1\), …, \(p_{t-1}\),\(p_t\)” 等于长度更小的后缀 “\(p_{j-t}\), \(p_{j-t+1}\), …, \(p_{j-1}\), \(p_j\)“呢?如果存在,那么这个t+1 便是next[ j+1]的值,此相当于利用已经求得的next 数组(next [0, …, k, …, j])进行P串前缀跟P串后缀的匹配。
我的代码
好像就是复制了上面两位的代码一样
# include <bits/stdc++.h>
# define MAXN 100
using namespace std;
void mktable(const char* temp, int* f) {
int n = strlen(temp);
f[0] = f[1] = 0;
for (int i = 1; i < n; i++) {
int j = f[i];
while (j && temp[j] != temp[i]) j = f[j];
f[i + 1] = temp[i] == temp[j] ? j + 1 : 0;
}
}
void kmp(const char* str, const char* temp, int* f) {
int n = strlen(str), m = strlen(temp);
mktable(temp, f);
int j = 0;
for (int i = 0; i < n; i++) {
while (j && temp[j] != str[i]) j = f[j];
j += (str[i] == temp[j]);
if (j == m) printf("%d", i - m + 1);
}
}
int f[MAXN];
char a[MAXN], b[MAXN];
int main() {
cin >> a >> b;
kmp(a, b, f);
return 0;
}